分かりやすい還元算(逆算)の教え方

パパ塾挑戦中、ウクレレ大好きレレパパです。

小学生には「移項」って理解しにくいみたいだね。
※本記事の作成時点:長女(小3)、次女(年長)
還元算(逆算)の問題を解くときには「移項」をします。
↓こういうの。
□+3=○
□=○-3
小学生は移項が苦手らしい
このような移項って、小学生には意外と難しいらしいですね。
↓例えば、こんなの。
○÷□=3
□=???
確かに、ぱっと見では式を変形できません。
もっと難しいのは……
でも、「小学生が移項を理解すること」よりも、もっと難しいことがあります。
それは、「小学生に移項を理解させること」。
僕も長女に移項のやりかたを教えたいのですが、どうやって教えるのが一番良いのか分かりませんでした。
自分が中学受験をしていないので、小学生にとって移項の何がそんなに難しいのかが理解できないのです。
ネットで教え方を調べてみたら……
そこで、ネット上の先達に習うことにしました。
そうすると、以下のような2通りの教え方があるようです。
【教え方A】線分図・面積図を使う方法
【教え方B】線分図・面積図を使わない方法
【教え方A】線分図・面積図を使う方法
1つ目は、中学受験生御用達の線分図・面積図を使う方法です。
和や差であれば線分図を使い、積や商であれば面積図を使います。
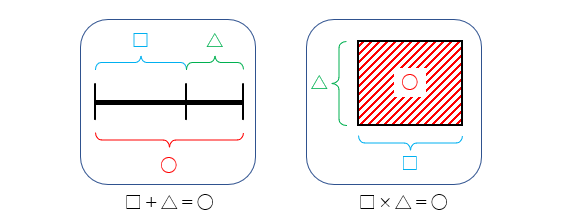
これは確かに教えやすい!
小学生にとっても使いやすい方法だと思います。
これでいいじゃん!
ですが、1つの問題が……

思考が途切れる!
数式の計算をしているときって、脳内の一時記憶メモリに色々と書き込みながら処理をしていると思います。
例えば、「この足し算が終わったら全体を7で割ろう」とか、「13で約分できそうだな」とか、頭の隅で考えながら計算をしています。
ですが、線分図や面積図を考えた瞬間に、その一時記憶メモリが全て消去されてしまうのです。
メモリが消去されないくらい線分図や面積図に慣れれば大丈夫なのかもしれませんが、一朝一夕にはできない芸当な気がします。
【教え方B】線分図・面積図を使わない方法
2つ目は、冒頭で紹介したような、いわゆる「移項」です。
□+3=○
□=○-3
僕のように中学受験をしていない層にとっては、この方がシンプルかつ万能だと思ってしまいます。
また、ずっと数式を目で追いながら計算を進めるため、途中で思考が途切れることもありません。
ただ、以下の2通りの場合については、小学生には少し複雑すぎるようです。
○-□=3
□=○-3
○÷□=3
□=○÷3
ネット上の先達によると、これらの2つについては公式として覚えてしまおう!という意見が散見されました。
ですが、上手く言えないですが、このような基本的な式変形を公式として覚えるのには抵抗があります。
特に長女なんかは、入試の本番で公式を忘れてしまいそう(笑)
我が家の方針
このように、教え方Aにも教え方Bにも、それぞれ一長一短あります。
そこで、我が家では、とりあえず両方教えることにしました。
両方教えてみて、使いやすい方を採用してもらおうと思います。
以上を踏まえ、例によってオリジナル教材を作りました。
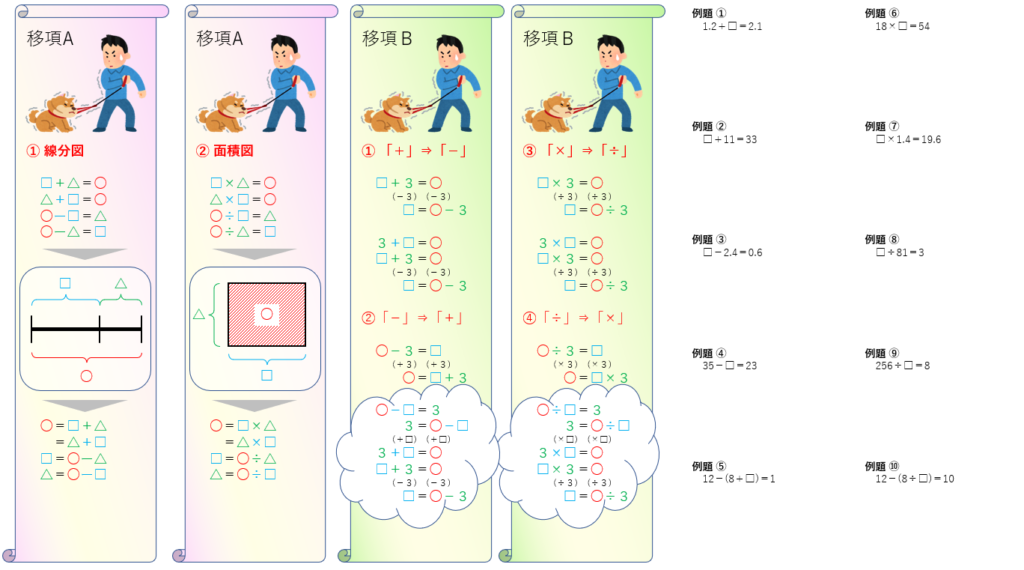
教え方AB併用がベストか?
オリジナル教材を作りながら、こう思いました。
【原則】
教え方Bのように移項する方法で教える。
【例外】
移項では教えにくい2つ(「6-□=3」「6÷□=3」)のみ、教え方Aのように線分図・面積図で考える。
という、教え方ABのハイブリッド方式がベストかも?
試しに長女に教えて、感想を聞いてみようと思います。

私も高校受験組だから難しさが分からない。
にほんブログ村

ブログランキングに参加しています!
一日一回、バナーを押して清き一票、応援お願いします!
※にほんブログ村のサイトに飛びます。














